The purpose of this post is to describe a side project I did to analyze SEC filing in an attempt to spot irregular values in 10Q filings.
Background
Benford’s Law
Benford’s law is a well known natural phenomenon discovered many many years ago in 1938 by physicist Frank Benford. Under certain key assumptions it relates that the probability distribution of the occurrence of the first and second digits of a list of numbers spanning multiple digits have been observed to follow a well observed distribution. Now for the statisticians out there there are key assumptions in which this natural 1st and 2nd digit distribution observation is valid and other cases where this is invalid. Often times folks will take these assumptions for granted and use Benford’s Law as a hard test when really its application in accounting has been a flag or notification that something should be further investigated. For example we shouldn’t be using Benford’s Law when the list of digits under investigation is too small (e.g. 11, 55, 155, 499) because the occurrence of the leading digits will be more biased. We will delve more into this importance later.
Edgar SEC:
Edgar stands for Electronic Data Gathering, Analysis, and Retrieval system. It is the digital collection of SEC filings where a user can pull up financial files of any company they desire and these documents are all publicly available. There are two means of access. One can use the Edgar SEC webpage to manually pull files or utilize their ftp service to more systematically retrieve files.
Edgar Central Index Key:
The SEC does not want bots constantly pinging their servers and retrieving files for good reason. This would create a load balancing nightmare. So to allow their servers and users to still retrieve information programmatically they created the Central Key Index or CIK. The CIK is a unique identifier foreign key that is ascribed to a company. For example if I wanted to download all the financial documents of Lehman Brothers I would first have to know the CIK that corresponds to that company. Once I have the CIK I can then use that key in the ftp to programmatically retrieve all past documents and current filings (which doesn’t make sense because Lehman Brothers no longer exists).
10Q Filings:
10Q filings are on of many files that companies are mandated to publish to the SEC in order to comply as a publicly traded company. Among these files are the quarterly earnings, expenditures, internal tradings, and other files. The 10Q files are of particular interest because often contain data that companies must publish and yet are not audited. 10K files on the other hand are annual files that contain expenditures, capital costs, cash flow, etc.. that are audited. This makes 10Q files more ripe for embellishment because there is pressure to meet quarterly expectations and the documents are not thoroughly audited compared to 10K files.
Training Dataset
There are known incidents of fraud all throughout the history of the stock market. The best part is that all these companies had to file SEC documents before, during, and after these incidents became known. So fraudulent companies like Enron, etc.. have known dates and readily available filings, in this case we were interested in 10Q filings, to serve as our “training” data set. I created a list of 10Q files corresponding to companies at a particular point in time known to have been conducting fraud.
Thesis
We will create a list of known 10Q documents pertaining to a period in time when companies that were audited and deemed to be conducting fraud. We will conduct Benford’s law on the numbers in these documents and compare their distributions against companies not identified as fraudulent in the same time period. We will try and use a diversified group of companies for both training and test groups. Ideally we would like to obtain an idea for the rate of false positives and true positives to understand the predictive ability of our small algorithm.
Method
All code is publicly available at my local github account.
Download SEC Indices
I successfully downloaded all SEC CIK’s into the form of a SQL database on my local drive.
def FTPRetrieve(Primary, Path, SavePath):
import ftplib
server="ftp.sec.gov"
user="anonymous"
password="YouEmailAddress@gmail.com"
try:
ftp = ftplib.FTP(server)
ftp.login(user,password)
except Exception,e:
print e
else:
#edgar/data/100240/0000950144-94-000787.txt
ftp.cwd("edgar/data/" + Primary + "/")
try:
ftp.retrbinary("RETR " + Path ,open(SavePath + Path, 'wb').write)
#ftp.retrbinary("RETR " + filename ,open(filename, 'wb').write)
ftp.quit()
except:
print "Error"
import sqlite3
import csv
import glob
def tosqlite(file):
with open(file) as f:
idx = csv.reader(f, delimiter='|')
for row in idx:
cur.execute('INSERT INTO idx (cik, cname, form, date, path) VALUES (?, ?, ?, ?, ?)', row)
#con = sqlite3.connect('~/DSTribune/Code/EdgarIndex/edgaridx.db')
con = sqlite3.connect('edgaridx.db')
with con:
con.text_factory = str
cur = con.cursor()
cur.execute('DROP TABLE IF EXISTS idx')
cur.execute('CREATE TABLE idx(Id INTEGER PRIMARY KEY, cik TEXT, cname TEXT, form TEXT, date TEXT, path TEXT)')
# for idxfile in glob.glob('~/DSTribune/Code/EdgarIndex/*.idx'):
for idxfile in glob.glob('*.idx'):
print idxfile
tosqlite(idxfile)
Download 10Q Training and Test Data sets:
From there I identified the companies I knew to have been fraudulent within a given date range. I observed that the years 2001 – 2004 contained a high frequency of known filing fraud and so focused on this time period. This would be my training dataset.
import sqlite3
import re
from FTPEdgar import FTPRetrieve
from ExtractNumbersV2 import BenfordsLaw
from datetime import datetime
tstart = datetime.now()
print tstart
#The following file paths are examples of locations that I locally saved my sqlite database, change to a place you see fit!
SavePath = r"/home/PycharmProjects/Edgar/EdgarDownloads/"
LedgerPath = r"/home/PycharmProjects/Edgar/"
conn = sqlite3.connect(r"/home/Code/EdgarIndex/edgaridx.db")
c = conn.cursor()
#------------------------------------------------------------------------
#Companies found to be fraudulent during period of study
#ENRON: 72859 (2001)
#Waste Mang: 823768 (1999)
#Worldcom: 723527 (2002)
#TYCO corp: 20388 (2002)
#HealthSouth 785161 (2003)
#Centennial Technologies 919006
#Peregrine Systems Inc 1031107 (2002)
#AOL: 883780
#AOL TimeWarner: 1105705 (2002)
#Adelphia Communications Corp: 796486 (2002)
#Lehman Brothers Holdings Inc: 806085 (2010)
#AIG: 5272 (2004)
#Symbol Technologies: 278352 (2002)
#Sunbeam Corp: 3662 (2002)
#Meryl Lynch and Co Inc: 65100
#Kmart: 56824 (2002)
#Homestore Inc: 1085770 (2002)
#Duke Energy Corp: 1326160 (2002)
#Dynergy: 1379895 (2002)
#El Paso Energy Corp: 805019 (2002)
#Haliburton: 45012 (2002)
#Reliant Energy Inc: 48732 (2002)
#Qwest Communications: 1037949 (2002)
#Xerox: 108772 (2000)
#Computer Associates: 356028 (2000)
#Unify Corp: 880562 (2000)
#compList = [72859, 823768, 723527, 20388, 785161, 919006, 1031107, 883780, 1031107, 883780, 1105705, 796486, 806085, 5272, 3662, 65100, 56824, 1085770, 1326160, 1379895, 805019, 45012, 48732, 1037949, 108772, 356028, 880562]
#Companies not idetnfied as fraudulent during period of study
#Intel: 50863
#Microsoft: 789019
#Starbucks: 829224
#Walmart: 217476
#Amazon: 1018724
#Qualcomm: 804328
#AMD Inc: 1090076
#Verizon: 1120994
#Ebay: 1065088
#Home Depot: 354950
#Geico: 277795
#Costco: 734198
#compList = [50863, 789019, 829224, 217476, 1018724, 1090076, 1120994, 1065088, 354950, 277795, 734198]
compList = [1321664, 92380, 18349, 1127999, 1171314, 78003, 789019, 91419, 716729, 318154, 814361, 318771, 796343]
for company in compList:
for row in c.execute("SELECT * FROM idx WHERE form = '10-Q' AND cik = '" + str(company) + "';"):#"' AND DATE(substr(date,1,4)||substr(date,6,2)||substr(date,8,2)) BETWEEN DATE(19960101) AND DATE(20040101);"):
print row[0], row[1], row[2], row[3], row[4], row[5]
ID = str(row[0])
Primary = str(row[1])
Company = str(row[2])
Document = str(row[3])
Date = str(row[4])
MyPath = str(row[5])
MyFile = re.search('\d+-\d+-\d+.txt',MyPath).group()
#print ID, Primary, Company, Document, Date, MyPath, MyFile
try:
FTPRetrieve(Primary, MyFile, SavePath)
except:
print "could not find " + Company
else:
BenfordsLaw(LedgerPath,SavePath,MyFile,Company,Date,Primary,ID,Document)
#c.execute("SELECT * FROM idx WHERE form = '10-Q';")
#print c.fetchall()
tend = datetime.now()
print tend
c.close()
Analyze each file after subsequent download:
While our system is downloading these 10Q filings (There are rate limits) we can actually use Python to simultaneously parse and analyze all numbers of interest within each 10K filing. This allows us to ping EDGAR at a sustainable rate while using that same cpu power to parse, analyze, and record results in a csv file. By combining the downloading and analysis on the same cpu we open the door for multiple instances or batch jobs if we want to do larger scale analysis in the future.
def BenfordsLaw(LedgerPath, SavePath, filename, Company, Date, Primary, ID, Document):
import math
import scipy.stats
import numpy as np
#Find values only with commas
import re
RawList = [re.findall(r'\d+[,]\d+',line)
for line in open(SavePath + filename)]
NoEmpty = filter(None, RawList)
DeleteIndex = []
AddIndex = []
#Then remove those commas
Counter = 0
for item in NoEmpty:
Counter += 1
if len(item) > 1:
for targetElement in range(1,len(item)):
AddIndex.append(item[targetElement])
DeleteIndex.append(Counter - 1)
NoEmpty = [i for j, i in enumerate(NoEmpty) if j not in DeleteIndex]
CleanNoEmpty = []
for i in NoEmpty:
CleanNoEmpty.append(i[0])
FinalList = CleanNoEmpty + AddIndex
CleanFinalList = []
numDist = [0,0,0,0,0,0,0,0,0]
for item in FinalList:
CleanFinalList.append(item.replace(',', ''))
counts = []
CleanFinalList2 = []
for number in CleanFinalList:
# i = "An, 10, 22"
last = number[-1]
secLast = number[-2]
pop = number[1]
# pop = 'n', the second character of i
if int(pop[0]) != 0 and last != 0 and secLast != 0 and len(number) >= 4:
counts.append(int(pop[0]))
numDist[int(pop)-1] = numDist[int(pop)-1] + 1
CleanFinalList2.append(number)
print CleanFinalList2
print counts
def Benford(D):
prob = (math.log10(D + 1) - math.log10(D))
return prob
chi2, p = scipy.stats.chisquare( counts )
msg = "Test Statistic: {}\np-value: {}"
print( msg.format( chi2, p ) )
from scipy import stats
from scipy.stats import ks_2samp
PList = []
DList = []
unifPList = []
unifDList = []
xk = np.arange(10)
xk = xk[1:10]
unifxk = np.arange(10)
pk = (Benford(1), Benford(2), Benford(3), Benford(4), Benford(5), Benford(6), Benford(7), Benford(8), Benford(9))
unifpk = (0.1197,0.1139,0.1088,0.1043,0.1003,0.0967,0.0934,0.0904,0.0876,0.0850)
custm = stats.rv_discrete(name='custm', values=(xk, pk))
unifCustm = stats.rv_discrete(name='custm', values=(unifxk, unifpk))
IterCt = 1000
for iter in range(IterCt):
R = custm.rvs(size=len(counts))
R = R.tolist()
placeholder = ks_2samp(counts, R)
PList.append(placeholder[1])
DList.append(placeholder[0])
unifR = unifCustm.rvs(size=len(counts))
unifR = unifR.tolist()
unifplaceholder = ks_2samp(counts, unifR)
unifPList.append(unifplaceholder[1])
unifDList.append(unifplaceholder[0])
AveP = sum(PList)/IterCt
AveD = sum(DList)/IterCt
unifAveP = sum(unifPList)/IterCt
unifAveD = sum(unifDList)/IterCt
DistPercent = []
for i in numDist:
DistPercent.append(float(i)/float(sum(numDist)))
print DistPercent
print AveP
print AveD
print unifAveP
print unifAveD
output = [AveP, AveD, unifAveP, unifAveD, len(counts), Company, Date, Primary, ID, Document]
#This script needs to be run twice. Once for the training set and once for the test set.
#fd = open(LedgerPath + "NonSuspected.csv",'a')
fd = open(LedgerPath + "NonSuspected.csv",'a')
for column in output:
if isinstance( column, int ):
fd.write('%.8f;' % column)
else:
fd.write('%s;' % column)
fd.write('\n')
fd.close()
The script above exports the results of the analysis as a csv. We run it once for the training dataset with known fraud and once again for the test list or companies not identified as fraudulent. The way we ascertained if the distributions of the 1st and 2nd digits followed the known Benford 1st and 2nd digit occurence distributions was to conduct a chi squared test of independence to determine the probability that the two distributions come from the same process. The null hypothesis is that the two distributions are independent of each other while the alternative hypothesis is that the two distributions originated from the same process and are not independent but are related. If the two samples are unlikely to be produced given the null hypothesis (they were created independent of each other) than we would expect a low probability or p-value under the null hypothesis. Often the scientific community will use a p-value of 0.05 or 5% as a rule of thumb however this will depend on the area of study as these p-value or significance thresholds can be empirically derived. What I am more curious about is if the distribution of p-values comparing the fraudulent vs. non-fraudulent group differs significantly for both the 1st and 2nd digit.
Results
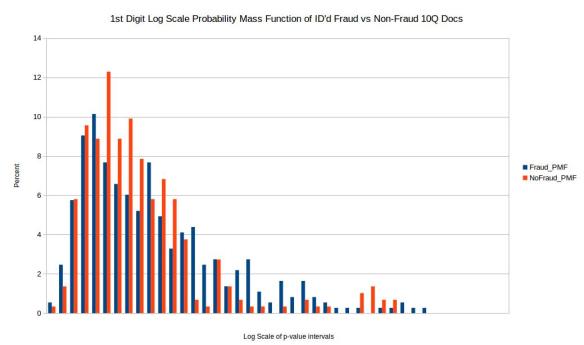
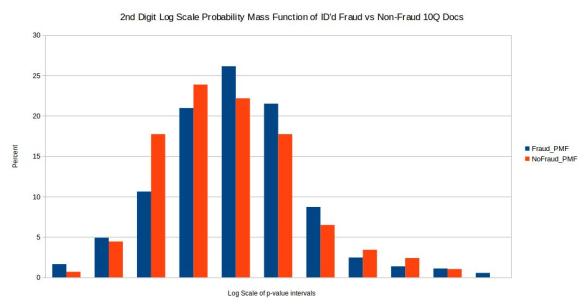
Before comparing the two samples I first eliminated p-values where the quantity of valid numbers within each filing were below 100 in order to eliminate any bias from small quantities of numbers in each filing. In order to compare the distribution of p-values for the chi squared comparison test I took a log scale base 10 of the p-values for both test and training set. I then setup intervals of 0, -0.5, -1, -1.5 all the way to -42 in order to create a probability mass function or PMF. The reason I wanted to do a PMF is because when directly comparing two distributions one should not compare histograms directly if the sample size for both samples are not exactly the same (which is often not the case). So to make up for this I took the percentage within each log base 10 range (0.5 increments) and created a PMF as seen above. Unfortunately the results come back pretty inconclusive. I would have hoped for two distinct and easily separable distributions however these results don’t visibly show that.
Conclusion
While Benford’s law is very powerful it may not be appropriate for 10Q documents. For one the algorithm works better on raw values and many of the values in the 10Q documents may be sums or output that resulted from operations on raw values. I think that Benford’s would work better on raw accounting logs that have more transaction data. Also I ran into a lot of numerical data points in 10Q files that were merely rounded estimates. I did my best to eliminate these in python. Finally Benford’s law works best when there is a wide range in the # digits.
Future
I think there is still potential to programatically analyze EDGAR files however 10Q files may not be close enough to the metal of company accounting necessary for the job. I am open to ideas though in the spirit of this analysis.
~Mr. Horn